Union
This is a synchronous temporal expression. It creates an implicit clock that is the result of the expression. The implicit clock ticks each time one of the clocks provided as parameter ticks. To ease the reading we have added a coincidence relation between the implicit resulting clock and an explicit clock named c3.
the CCSL specification:
Simulation results:
The Union expression simulation is represented on the next picture.
On the bottom right, the clock domain is represented; here, both clocks provided as parameters of the expression are sub clocks of the clock that results from the expression. The resulting clock is named IC6 (ImplicitClock and a unique number for the simulation). Its actual name can be seen in a message when the mouse moves over the state (as shown on the picture)

This expression provides a solution that is totally ordered as shown in the following picture showing also instant relations.

Intersection
This is a synchronous temporal expression. It creates an implicit clock that is the result of the expression. The implicit clock ticks each time the two clocks provided as parameters tick simultaneously. To ease the reading we have added a coincidence relation between the implicit result clock and an explicit clock named c3.
the CCSL specification:
Simulation results:
The Intersection expression simulation is represented on the next picture.
On the bottom right, the clock domain is represented; here, the resulting clock is a subClock of the two clocks provided as parameters of the expression
The resulting clock is named IC7 (ImplicitClock and an unique number for the simulation). Its actual name can be shown in a message when the mouse moves over the state (as shown on the picture)
This expression provides a solution that is partially ordered as shown in the following picture where the instant relations are displayed.
However, for readability reasons, we decided to not represent the exclusion relation that holds between C1 and C2 when C3 does not tick

Wait
This is a synchronous temporal expression. It creates an implicit clock that is the result of the expression. The implicit clock ticks only once after a specific number of ticks of the clock provided as a parameter. After its unique tick, the implicit clock dies (it cannot tick anymore). To ease the reading we have added a coincidence relation between the implicit result clock and an explicit clock named c2.
the CCSL specification:
Simulation results:
The Wait expression simulation is represented on the next picture. On important point is that after its sole tick, the implicit clock dies (represented by a yellow line on the picture). Because c2 is coincident with the implicit clock, then it dies at the same time than the implicit clock.
On the bottom right side, the clock domain is represented; here, the resulting clock is a subclock of the clock provided as parameter

Defer
This is a mixed temporal expression. Like any expression, it creates an implicit clock that is the result of the expression. To understand how it works, the reader must think about its personnal calendar. The expression takes a sequence as a parameter. A sequence has a finite part and a infinite part (the one between the parenthesis).
Each time the ‘BaseClock’ (i.e., c1 in the example) ticks, a meeting for the next ‘n’ ticks of the ‘DelayClock’ (i.e., c2) is taken. where ‘n’ is the current number in the sequence.
If the sequence has an empty infinite part, the implicit clock dies after its last tick.To ease the reading we have added a coincidence relation between the implicit result clock and an explicit clock named res.
The first CCSL specification (with an infinite part):
Simulation results:
On the picture below, the first tick of clock c1 schedules a tick of the result after one tick of c2. The second tick of c1 schedules a tick of the result after 6 ticks of c2. Finally, all other ticks of c1 schedule a tick of the result after 3 ticks of c2. On the picture, we can see that the third tick of c1 has caused the second tick of the result while the second tick of c1 has caused the third tick of the result. When two ticks are scheduled at the same tick, everything is like if only one were scheduled. This is exactly like sometimes in your calendar, you have meetings which are scheduled from a long time and some others are added just before the actual date.
On the bottom right, the clock domain is represented; here, the resulting clocks is a subclock of the ‘DelayClock’ (i.e., c2) and the ‘BaseClock’ (i.e., c1) precedes the implicit clock.

the second CCSL specification (with an empty infinite part):
/*
* res = c1 defer by 1; 3 ( 6 )
* @author: Julien DeAntoni
* date : Mon july 18th 2011
*/
ClockConstraintSystem MySpec {
imports {
import “ccsl:kernel” as kernelLib ; //add the kernel constraints to your specification
}
entryBlock main
Block main {
Clock c1
Clock c2
Clock res
Sequence s1 : IntegerSequence =
un = 1;
six = 6
Expression myDefer = Defer( BaseClock -> c1, DelayClock -> c2, DelayPatternExpression -> s1)
Relation r1[Coincides](Clock1 -> c3, Clock2 -> c1wait5 )
}
}
Simulation results:
TODO
The defer expression that causes the death simulation is represented on the next picture. The implicit clock dies after its last tick. Because res coincides with the implicit clock, then it dies at the same time than the implicit clock.
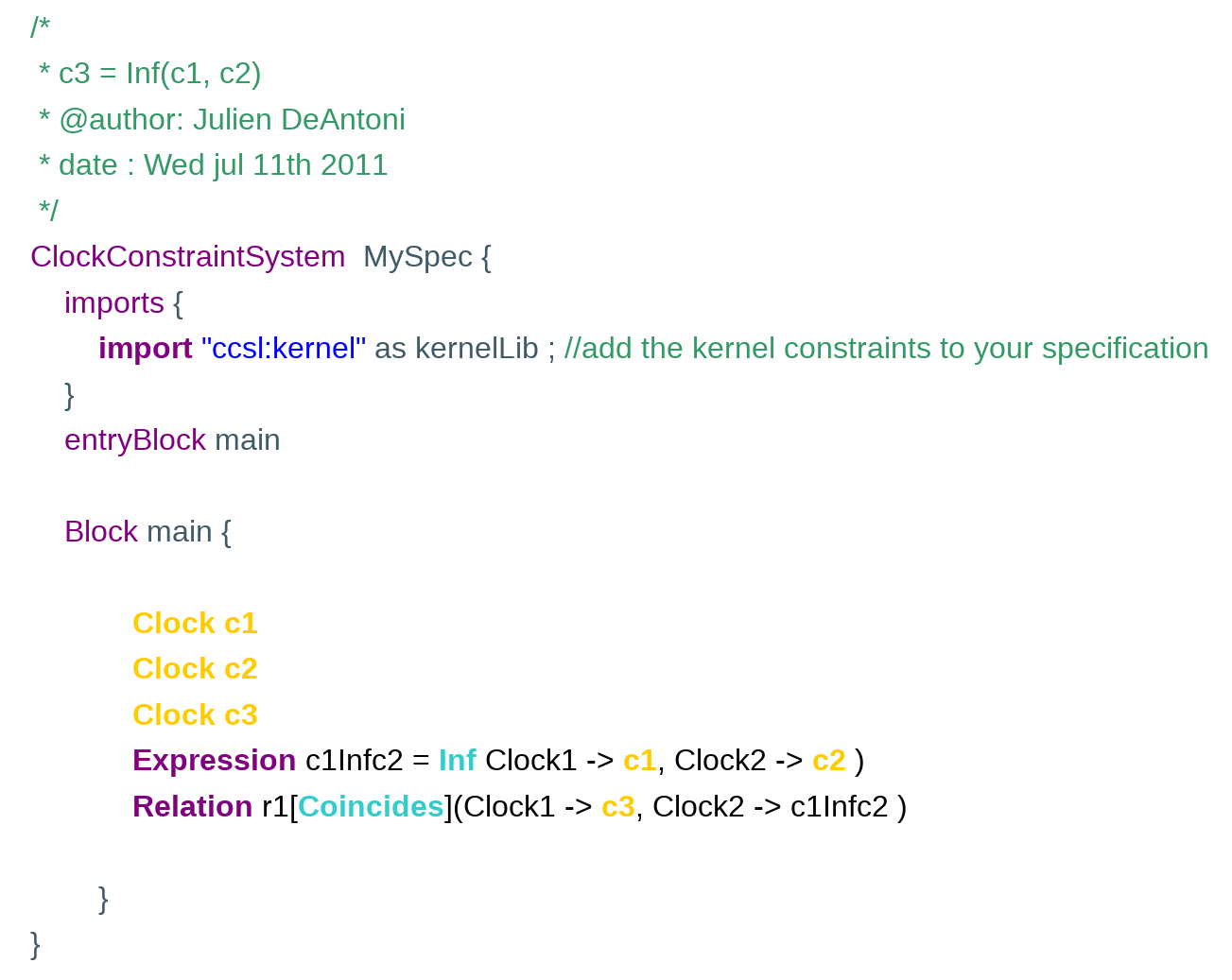
Inf
This is both a synchronous and an asynchronous temporal expression. It creates an implicit clock that is the result of the expression. The implicit clock ticks in coincidence one of the clock provided as a parameter. More precisely, it ticks with the one that precedes the other. In the following, to ease the reading we add a coincidence relation between the implicit result clock and an explicit clock named c3.
the CCSL specification:
Simulation results:
An Inf expression simulation is represented on the next picture. The four first ticks of the implicit clock tick with c1 while the others ticks coincide with c2. Moreover, the precedence relation is explicitly provided by timesquare and shown on the picture.
On the bottom right, the clock domain is represented; here, a symbolique clock that represents the union of c1 and c2 is represented (so c1 and c2 are both subclock of the union clock). The only thing know is that the implicit clock is then a subclock of the union clock.

Note that this expression provides a solution that is partially ordered as show in the previous picture where the instant relations are displayed.
Sup
This is both a synchronous and an asynchronous temporal expression. It creates an implicit clock that is the result of the expression. The implicit clock ticks in coincidence one of the clock provided as a parameter. More precisely, it ticks with the one that does not precede the other. In the following, to ease the reading we add a coincidence relation between the implicit result clock and an explicit clock named c3.
the CCSL specification:
Simulation results:
A Sup expression simulation is represented on the next picture. The six first ticks of the implicit clock tick with c2 while the others ticks coincide with c2. Moreover, the precedence relation is explicitly provided by timesquare and shown on the picture.
On the bottom right, the clock domain is represented; here, a symbolique clock that represents the union of c1 and c2 is represented (so c1 and c2 are both subclock of the union clock). The only thing know is that the implicit clock is then a subclock of the union clock.

Note that this expression provides a solution that is partially ordered as show in the previous picture where the instant relations are displayed.
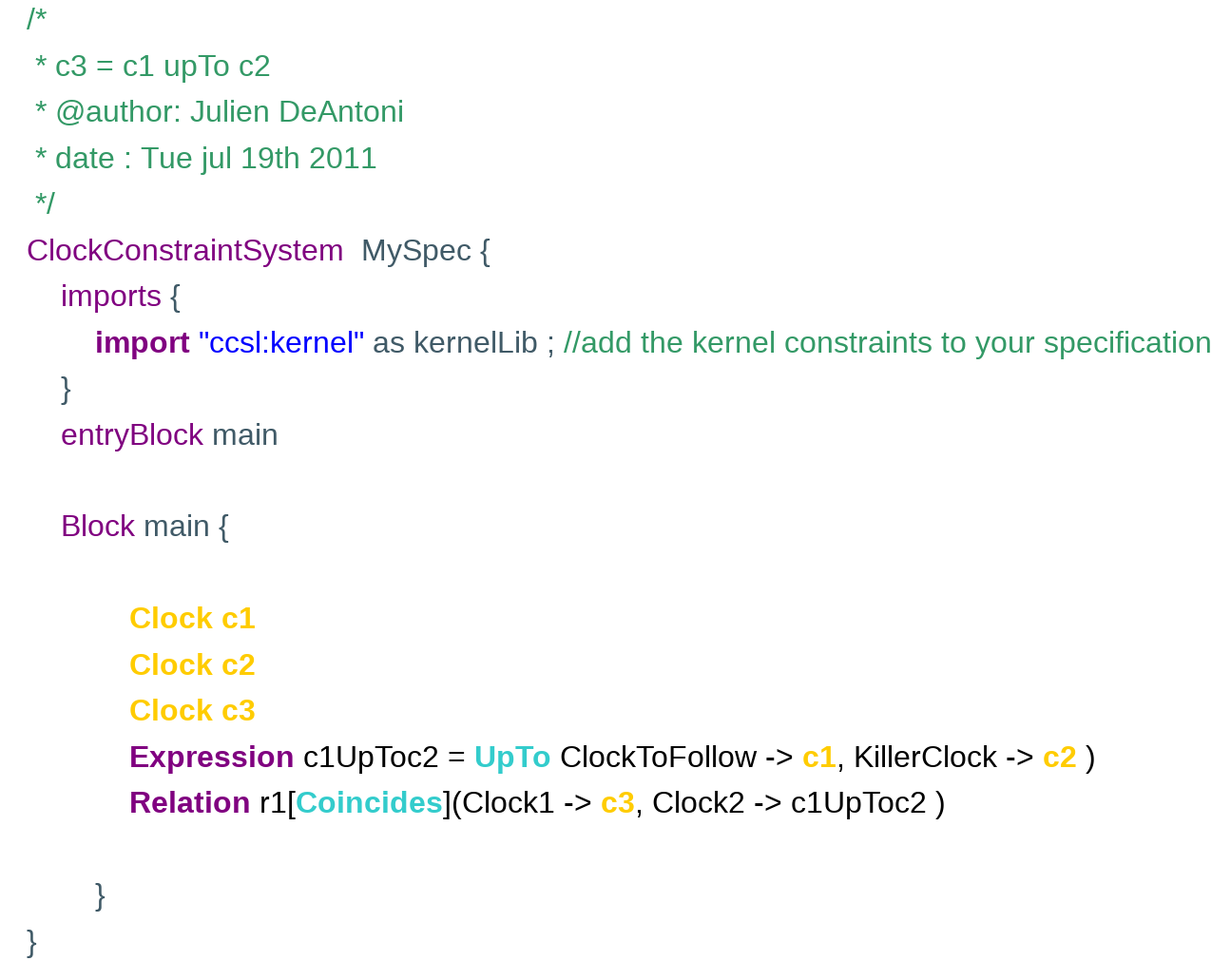
UpTo
This is both a synchronous and an asynchronous temporal expression. It creates an implicit clock that is the result of the expression. The implicit clock ticks in coincidence with ‘ClockToFollow’ (ie c1 in the example) until ‘KillerClock’ (ie c2) ticks. Once c2 ticked, the implicit clock is dead. Note that the death is propagated by the coincidence relation so that, in the example, c3 dies at the same time than the implicit clock.
the CCSL specification:
Simulation results:
An UpTo expression simulation is represented on the next picture. The two first ticks of the implicit clock tick in coincidence with c1 until the first tick of c2. Once again, the resulting partial order is provided by TimeSquare and shown on the timing diagram.
On the bottom right, the clock domain is represented; here, the implicit clock is subClock of c1 and c2 kills the implicit clock.

Concatenation
Concatenation is surely the most complicated expression. However the principle is quite simple. As all expressions, it creates an implicit clock that is the result of the expression.
The expression takes two arguments. The implicit clock ticks in coincidence with the first argument ‘LeftClock’ (ie c1 in the example) until the ‘LeftClock’ dies. After the die of the ‘LeftClock’, the implicit clock ticks in coincidence with the ‘RightClock”. Note that, if the ‘RightClock’ is not used elsewhere in the specification, its birth coincides with the dead of the ‘LeftClock’. Finally, it can be complex to understand because, as explain at the end of this page, the concatenation can be recursive.
A simple example is given below where the ‘LeftClock’ is an expression that dies (ie a wait expression). The ‘RightClock’ birth coincides with the ‘LeftClock’ dead.
Once c2 ticked, the implicit clock is dead. Note that the death is propagated by the coincidence relation so that, in the example, c3 dies at the same time than the implicit clock.
the CCSL specification:
Simulation results:
The simulation of the previous example is represented on the next picture. The first ticks of the implicit clock coincidences with the 5th tick of c1 and the second one with the 11th tick of c1 (the 6th that follows the death of the ‘LeftClock’). Moreover, as you can see, when the ‘RightClock’ dies, it simultaneously implies the death of the implicit clock.
On the bottom right, the clock domain is represented; here, the implicit clock is a sequence of two clocks. The sequence is a specific kind of subclocking.

It is important to notice that, without the concatenation in the previous specification, the result of c1wait6 would not be the same because its birth would be the beginning of the simulation. In this case the simulation would be:

TODO recursive concatenation